3.3.9 Member index

Member index — нахождение индекса элементов одного множества, встречающегося в другом множестве.

1) Set - данные для поиска;
2) Member - элементы, индексы которых необходимо найти в Set.
3) Index - индексы элементов Member, найденных в Set.
4) Count - встречаемость элементов Memeber в множестве Set.

Примеры

В некоторых случаях необходимо выяснить индекс того, или иного элемента, списка элементов или даже целых веток дерева данных. В этом случае следует использовать Member Index.

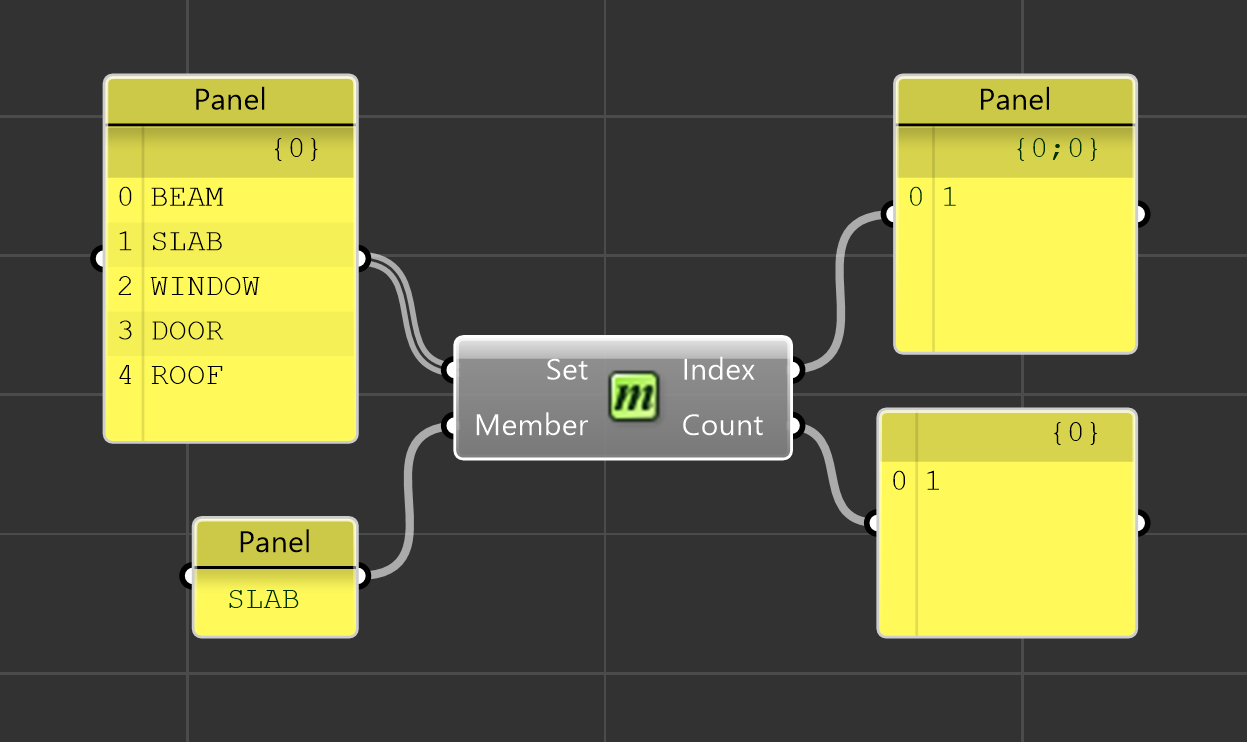
Обратите внимание на изображении выше, что среди списка, поданного во входной разъём Set был найден индекс элемента SLAB. В изначальном списке он имеет индекс 1 и встречаемость этого элемента равно 1.

В следующем примере выбирается список элементов, для выяснения их индексов:

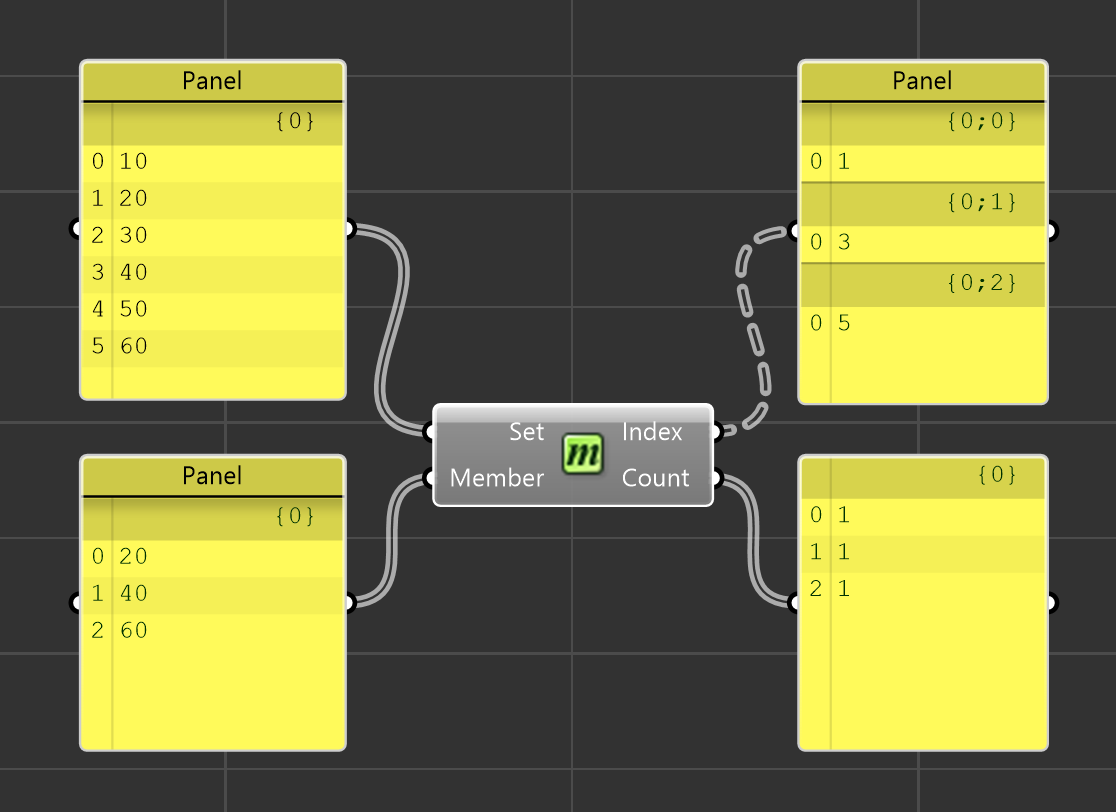
При поиске более 1 элемента Member в множестве Set в Index выводятся индексы каждого элемента поданного списка Member.

Тоже самое касается не только текста для поиска, но и численных значений:

При помощи Member Index можно искать индексы элементов в некоторых геометрических объектах, таких как точки. Представьте себе некоторую ситуацию, в которой, предположим есть некоторый список точек (не важно на одной они плоскости, или в пространстве):

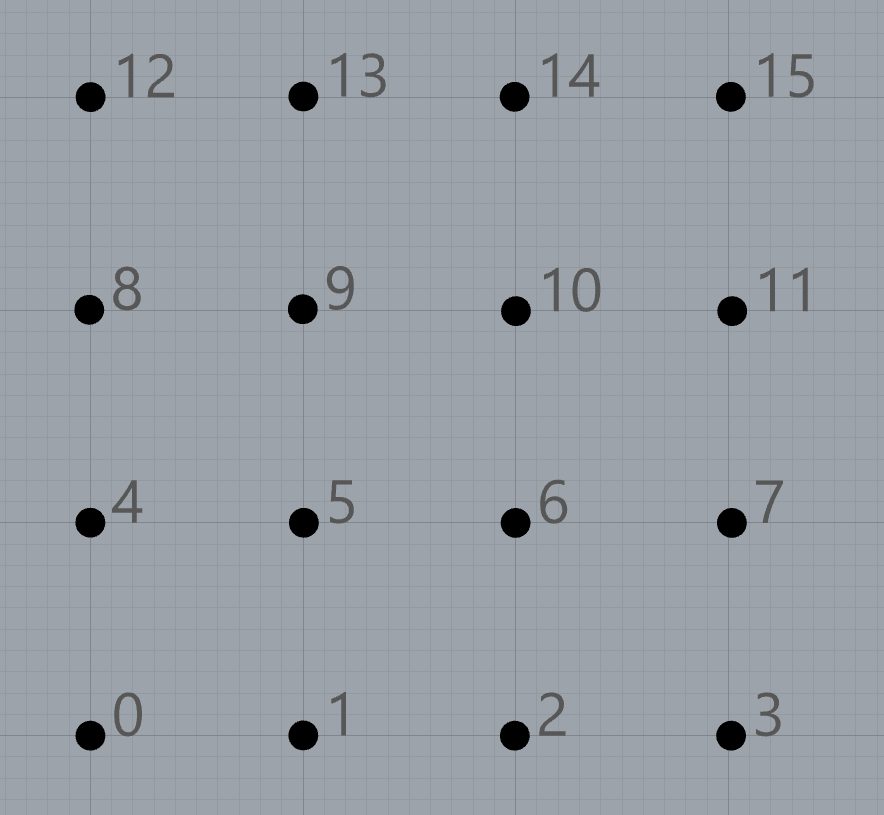
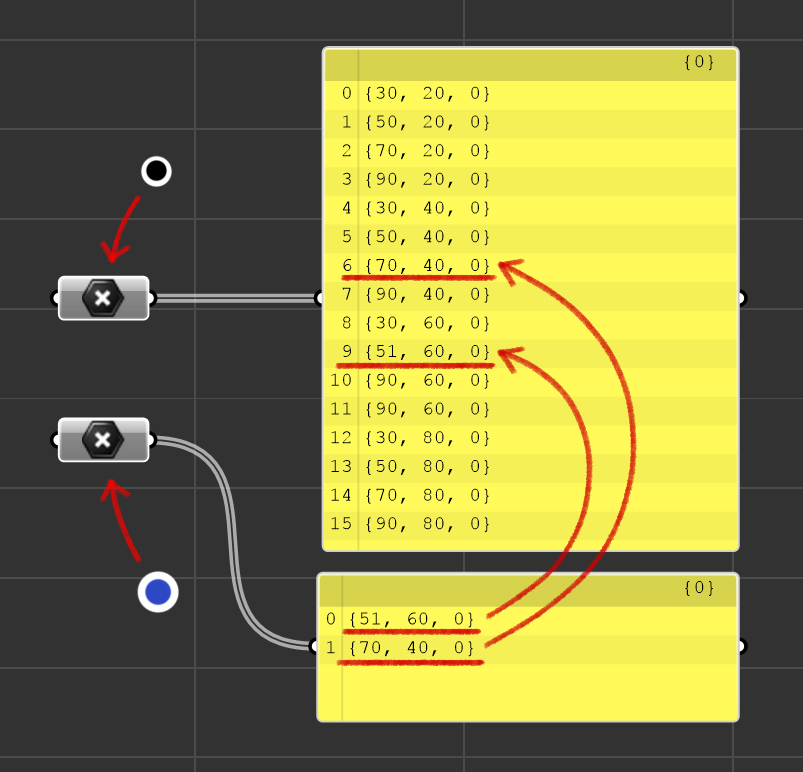
На изображении выше специально поставлены индексы точек. Представим себе, что в это пространство точек поставлены дополнительно 2 точки синего цвета в точности на тоже самое место (координаты совпадают), в которых находятся точки чёрного цвета:

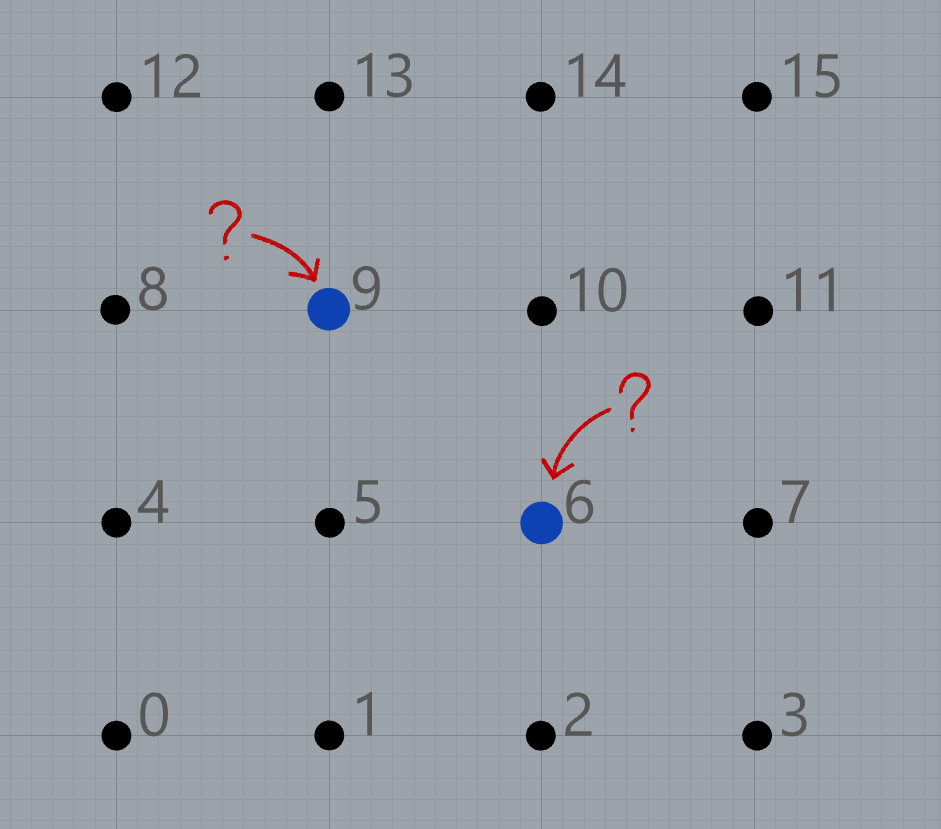
И так, необходимо найти индексы синих точек в списке чёрных точек. В данном случае, конечно, можно воспользоваться специальным нодом — Closest Point, однако в данном случае так же сработает Member Index:

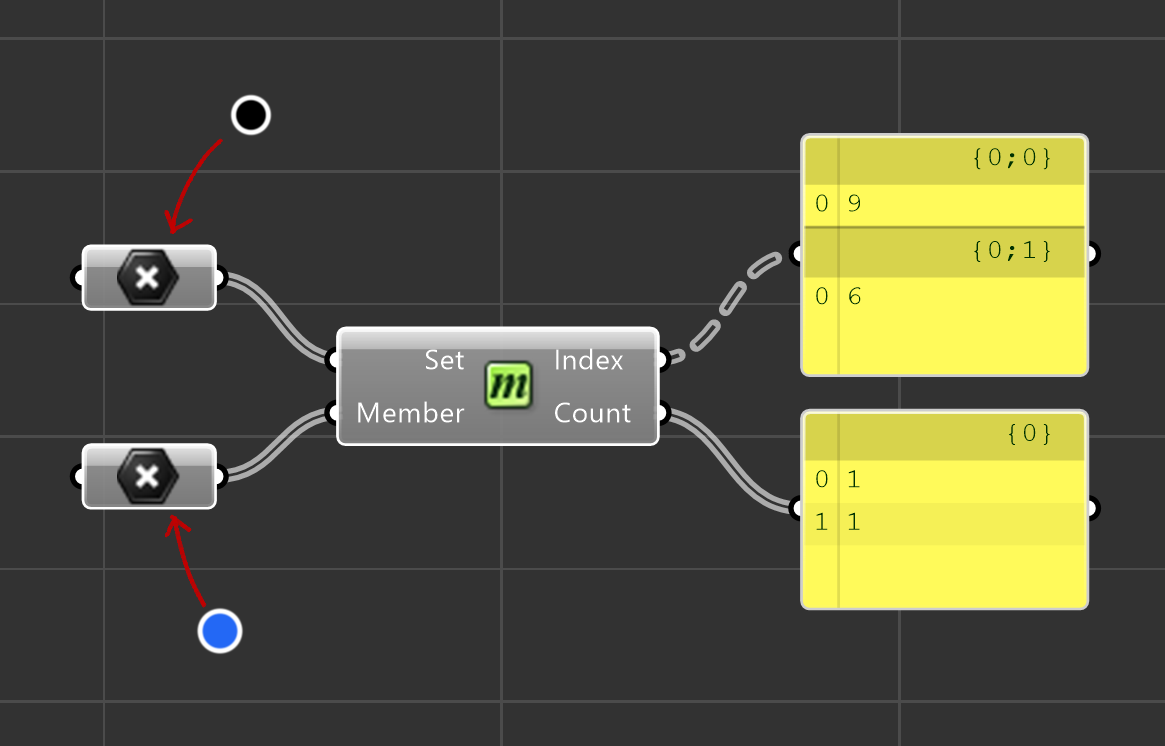
Важнейший момент в данном случае заключается в текстовом описании точки. Как вы можете знать, точка в Grasshopper описывается как набор из 3-х координат: X, Y и Z. Они записываются именно в таком порядке. В списке Grasshopper точка записывается в фигурных скобках: {x, y, z}. Например точка, находящаяся в самом центре координат выглядит так: {0,0,0}, это значит, что координата X = 0, Y = 0 и Z = 0.

Все эти уточнения нужны для объяснения каким образом Member Index нашёл пару синих точек в списке чёрных точек. Дело именно в текстовом описании точек. В панели всё представляется в текстовом виде, поэтому при помощи Member Index можно делать поиск элементов в текстах.

Задача 1

Дано: композиция из прямоугольных поверхностей. Найдите при помощи Member Index индекс прямоугольника с площадью равной 1407.

Скачайте файл Grasshopper и решите в нём задачу.

Задача 2

Дано: набор из панелей, размещённых вертикально. Порядок в панелях нарушен, т.е. индексы панелей размещены в случайном порядке. Необходимо при помощи Member Index выбирать любой горизонтальный ряд панелей. На изображении выбран предпоследний ряд (синее выделение):

Скачайте файл Grasshopper и постройте скрипт между начальным нодом Brep и конечным нодом, визуализирующим цвета панелей (Custom Preview).

При затруднении смотрите видео ответ на задачу ниже.

Задача 3

Дано: набор дублирующихся цифр или символов, расположенных в некотором списке. Список может быть вида 1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4..., так же и 150,150,150,220,220,220,400,400,400. Количество не имеет значения, символы могут меняться, важно то, что они дублируются. Небходимо сгруппировать все значения по принципу повторяемости. Результат должен быть как на изображении ниже (каждая группа символов в своей ветке) (в данной задаче используется нод Create Set):

Скачайте файл Grasshopper и постройте скрипт между начальным нодом и конечным нодом.

При затруднении смотрите видео ответ на задачу ниже.